
분할 정복
병합 정렬을 학습하기 전에 분할정복에 대해 먼저 알아보자.
분할 정복(Devide and Conquer)이란, 문제를 나눠서 각각을 풀고 다시 합병해서 답을 도출하는 알고리즘이다.
총 Devide, Conquer, Combine의 스텝으로 이루어지며
Devide는 현재 문제가 분할이 가능할 때, 2개 이상의 문제로 나누고
Conquer는 Devide를 통해 나눈 문제가 여전히 분할이 가능하면, 분할된 문제에 재차 Devide를 수행함을 의미한다.
Combine은 devide and conquer를 수행하고 더이상 나눠지지 않는 문제를 합병해 답을 도출하는 과정을 말한다.
분할 정복을 채택한 알고리즘에는 대표적으로 병합 정렬, 퀵 정렬 등이 있으며 이미 퀵 정렬은 다루었으니 병합 정렬을 살펴보자.
병합 정렬
병합 정렬이라고도 하고, 합병 정렬이라고도 한다.
퀵정렬과 동일하게 O(NlogN)의 시간복잡도를 가지는 알고리즘이다.
퀵정렬이 데이터가 편향 될 가능성이 있음과는 달리,
병합 정렬은 데이터를 항상 정확히 반씩 나누기 때문에 최악에도 O(NlogN)을 보장한다.
분할 정복이 나눠서 풀고 다시 합병해서 답을 도출한다고 했는데, 이를 토대로 병합정렬을 구현할 수 있다.
병합 정렬의 과정은 다음과 같다.

1. 배열을 반으로 나눈다.
2. 배열이 더이상 나눠지지 않을 때 까지 나눠진 배열에 1번 과정을 반복한다.
3. 크기가 1인 각 배열을 두개씩 묶어서 합쳐주며, 크기가 2인 배열로 만들어준다. 이 때 하나의 배열로 만들면서 정렬을 수행한다.
4. 병합한 배열이 N의 크기를 가질 때 까지 3번과 동일하게 병합 정렬을 수행한다.
gif를 통해 알아보기
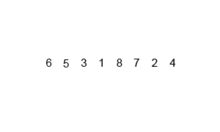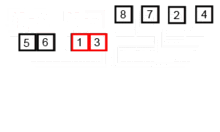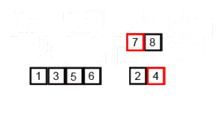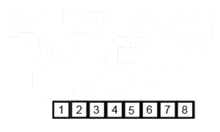
병합 정렬을 JS를 이용해 구현하기
function mergeSort(arr, start, end){
if(start < end){
const mid = Math.floor((start + end) / 2);
mergeSort(arr, start, mid);
mergeSort(arr, mid+1, end);
merge(arr, start, mid, end);
}
}
function merge(arr, start, mid, end){
let i = start;
let j = mid + 1;
let idx = start;
while(i <= mid && j <= end){
sortedArray[idx++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
}
if(i > mid){
for(let t=j; t<=end; t++){
sortedArray[idx++] = arr[t];
}
} else{
for(let t=i; t<=mid; t++){
sortedArray[idx++] = arr[t];
}
}
for(let t=start; t<=end; t++){
arr[t] = sortedArray[t];
}
}
const array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8];
const length = array.length;
const sortedArray = Array.from({length}, ()=>0);
mergeSort(array, 0, length - 1);
console.log(array); // [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]병합 정렬의 시간 복잡도
데이터 N개에 대해서 2*N개의 공간이 필요하므로 공간복잡도는 O(N)이며,
시간복잡도는 최선, 최악 모두 O(NlogN)을 보인다.
단계마다 데이터가 항상 반으로 나뉘고, 2배씩 증가하므로 단계의 크기가 logN을 유지하게 된다.
또한 정렬에 필요한 수행시간은 데이터 갯수인 N을 요구하므로, O(NlogN)을 나타나게 되는 것이다.
정렬 수행 시간이 N인 이유는 다음과 같다.

step1에서 크기가 1인 배열을 합칠 때 각 인덱스를 i, j로 조회하여 [7], [3] => [3, 7]의 배열을 만든다.
step2에서 크기가 2인 배열을 합칠 때 각 인덱스를 i, j로 조회하여 [3, 7], [2, 16] => [2, 3, 7, 16] 의 배열을 만든다.
step 1,2에서 합치기 전의 두 배열의 특징은 이전 과정에 의해 이미 정렬 된 배열인 것이고,
배열 각각을 i,j 인덱스를 통해 처음부터 끝까지만 순회하면 새로운 정렬된 병합 배열을 만들 수 있기 때문에 비교작업을 총 N번만 수행하면 된다.
각 스텝마다 총 N번의 비교 수행이 이루어지며, 병합의 스텝은 데이터가 절반씩 줄어드므로 logN번을 수행하게 된다.
장점
안정 정렬에 속한다.(=중복 값이 입력 순서와 동일한 정렬 순서를 보장한다.)
최악의 경우에도 O(NlogN)의 성능을 보장한다.
단점
별도의 배열 공간을 필요로한다. (제자리 정렬이 아니다.)
무조건 절반으로 분할하므로, O(NlogN)에서 성능이 달라지지 않는다.
'DS & Algorithm > theory' 카테고리의 다른 글
| 계수 정렬(Counting Sort) 이란 (0) | 2022.02.07 |
|---|---|
| 퀵 정렬(Quick Sort) 이란 (0) | 2022.02.07 |
| 삽입 정렬(Insertion Sort) 이란 (0) | 2022.02.04 |
| 선택정렬(Selection Sort) 이란 (0) | 2022.02.04 |
